显式积分与隐式积分

显式积分：步进具有预测能力，使用当前步参数预测出下一步所有参数
$y_{t+1} = y_{t} + \Delta {t} y^{'}_t$
隐式积分：隐式积分具有自我矫正能力，它使用下一步的参数矫正当前步参数
$y_{t+1} = y_{n} + \Delta {t} y^{'}_{t+1}$

常用的数值积分

考虑泰勒展开等价写法

显式积分

显式欧拉法
对位置 x(t), 做一阶泰勒展开
$x(t + \Delta t) = x(t) + x^{'}(t) \Delta t = x(t) + v(t) \Delta t$
$=>$
$v_{t+1} = v_{t} + a_{t} \Delta t$
$x_{t+1} = x_t + v_t\Delta t$
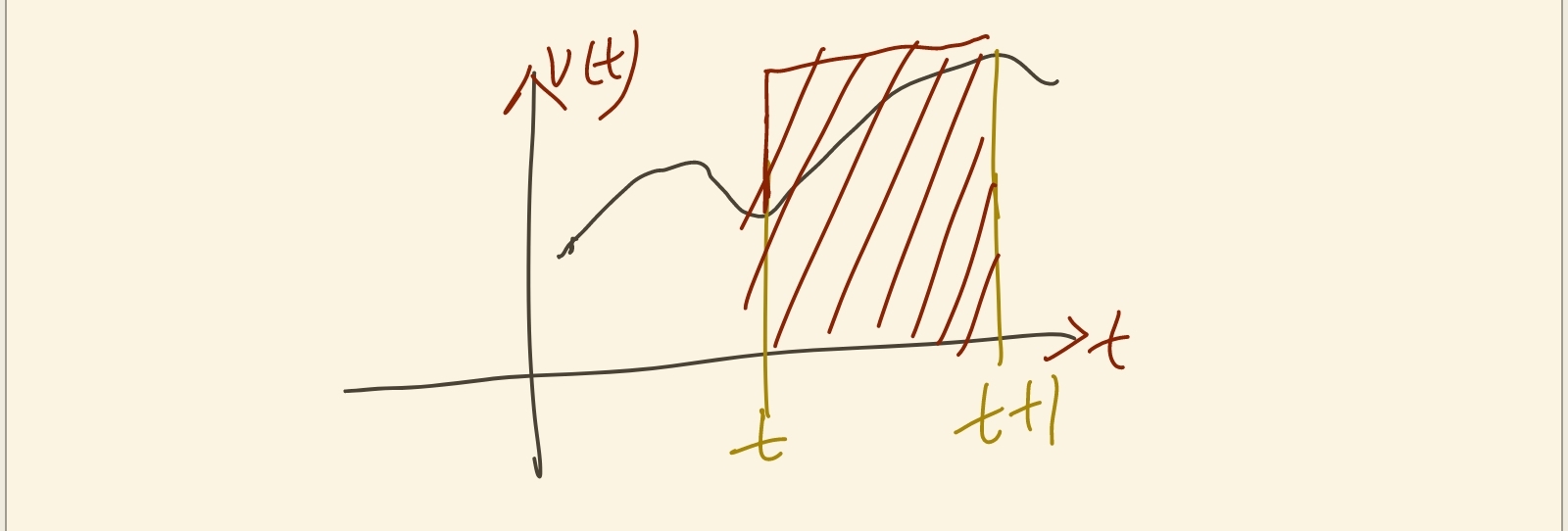
显然这里 x(t) 是一阶泰勒展开，使用矩形面积近似曲面面积，误差是二阶的，如下，

##隐式积分##
显示积分稳定性和步长关系较大，当步长取较大值时数值可能直接爆炸，这点可参考微分方程的数值处理，而隐式积分能很好的解决这一问题。

隐式欧拉
显式欧拉使用前向差分近似导数，而隐式欧拉采用后项差分近似导数。

半隐式积分

半隐式欧拉
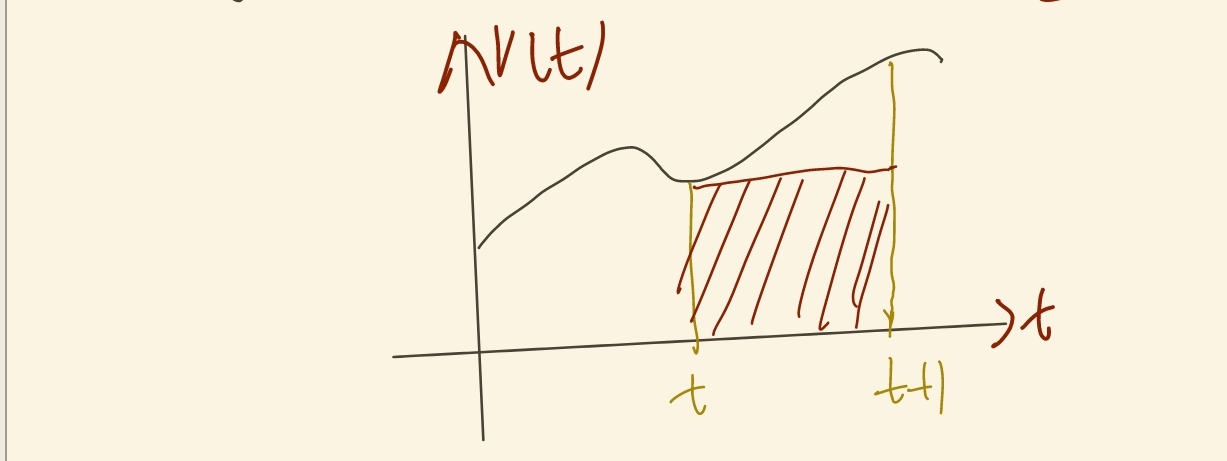
上面显式欧拉法，使用时步开始的函数值作为矩形高度，而半隐式欧拉采用时步结束时的值作为矩形高度（速度 v(t+1)），把上面的一阶泰勒展开修改为$x(t + \Delta t) = x(t) + x^{'}(t+1) \Delta t = x(t) + v(t) \Delta t$
$v_{t} = v_t + a_t\Delta t$
$x_{t+1} = x_t + v_{t+1} \Delta{t}$
示意图如下，误差也是二阶的