动画曲线-沿曲线运动

游戏中常常需要对一条曲线进行均匀采样以达到匀速运动，比如相机沿轨道匀速运动。下面说明
A Primer on Bézier Curves, Moving Along a Curve with Specified Speed - Geometric Tools
两篇文章给出的方案。

A Primer on Bézier Curves

A Primer on Bézier Curves 采用取样分割的思路对原曲线，按照较小的插值步长进行分割，保证两点之前的直线距离近似于曲线距离，如下图所示

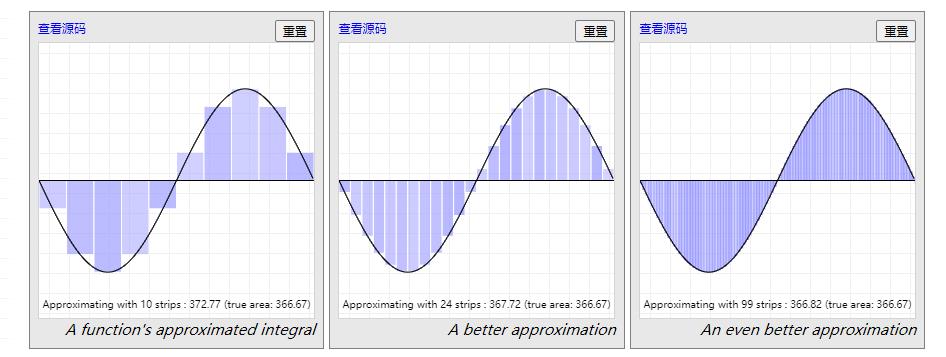
上述方案可以很方便的求出任意一个采样点 sample_i 距离曲线起点的长度 sample_len。
当需要获取曲线上距离起点指定长度 len 的位置 p 时，假定所有采样点中 sample_k 长度最接近 len, 那么 sample_k 所在位置即为所求位置 p。（显然可以通过二分快速从所有采样点中找到 sample_k）
缺点
这种方法需要大量采样才能保证相邻采样点直线距离与曲线距离近似，因此内存占用高，并且计算量与采样点数成正比
当曲线动态变化时，需要更新大量的或者所有的采样点曲线长

Moving Along a Curve with Specified Speed - Geometric Tools

假定已知：
1 插值曲线函数为 Q(t) = at^3 + bt^2 + c*t + d (a,b,c,d 为已知参数，t 为插值系数)，
2 另有对于 Q(t) 其曲线长函数为 AreLen(t)
问题：
求曲线上一点 p 的位置，且 p 点距离曲线起点曲线长度为 len
如何求解：
由于曲线长函数已知为 AreLen(t), 那么只要求出长度为 len 时的插值系数 t，然后再将 t 代入 Q(t) 求出的点位就是 p 点。
但现在的问题在于我们仅仅已知插值曲线函数 Q(t)，因此首先要求的就是 AreLen(t)。

曲线上任意一点的曲线长如何求解
对一段曲线无限分割后，用切线长近似曲线长，然后积分得到曲线长，或者按照 Moving Along a Curve with Specified Speed - Geometric Tools 中的推导，最终都能得到弧长表达式如下，$\mathbf{Y} 是一个参数方程，\mathbf{Y} = (x(t), y(t))$

对于上面的 Q(t), 求出其导数 D(t), 三维空间下有 $AreLen(t) = \sqrt{D(t).x^2 + D(t).y ^ 2 + D(t).z ^2}$, 最终 $s = g(t) = \int_0^t AreLen(\tau) \, {d}\tau$.
如何找到曲线长对应的插值系数 t
现在有 $s = AreLen(t)$ , 已知曲线长 s 求 t, 现在的问题是 AreLen(t) 反函数很难求，或者说压根求不出来，因此考虑数值方法求 t。
定义函数 $F(t) = g(t) - s$, 牛顿迭代法有

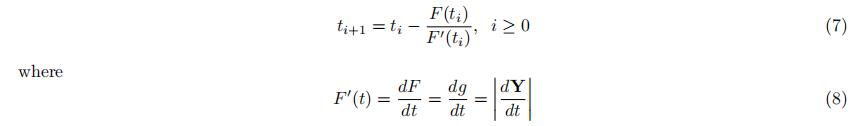
注意到上面需要求 $F(t_i)$ 可以参考下面这两篇文章采样数值积分的方法求解
【数值计算之二】数值积分之牛顿——科斯特公式：梯形、辛普森、辛普森3/8和布尔 & 高斯积分公式：勒让德、切比雪夫、拉盖尔和埃尔米特
曲线上的匀速运动
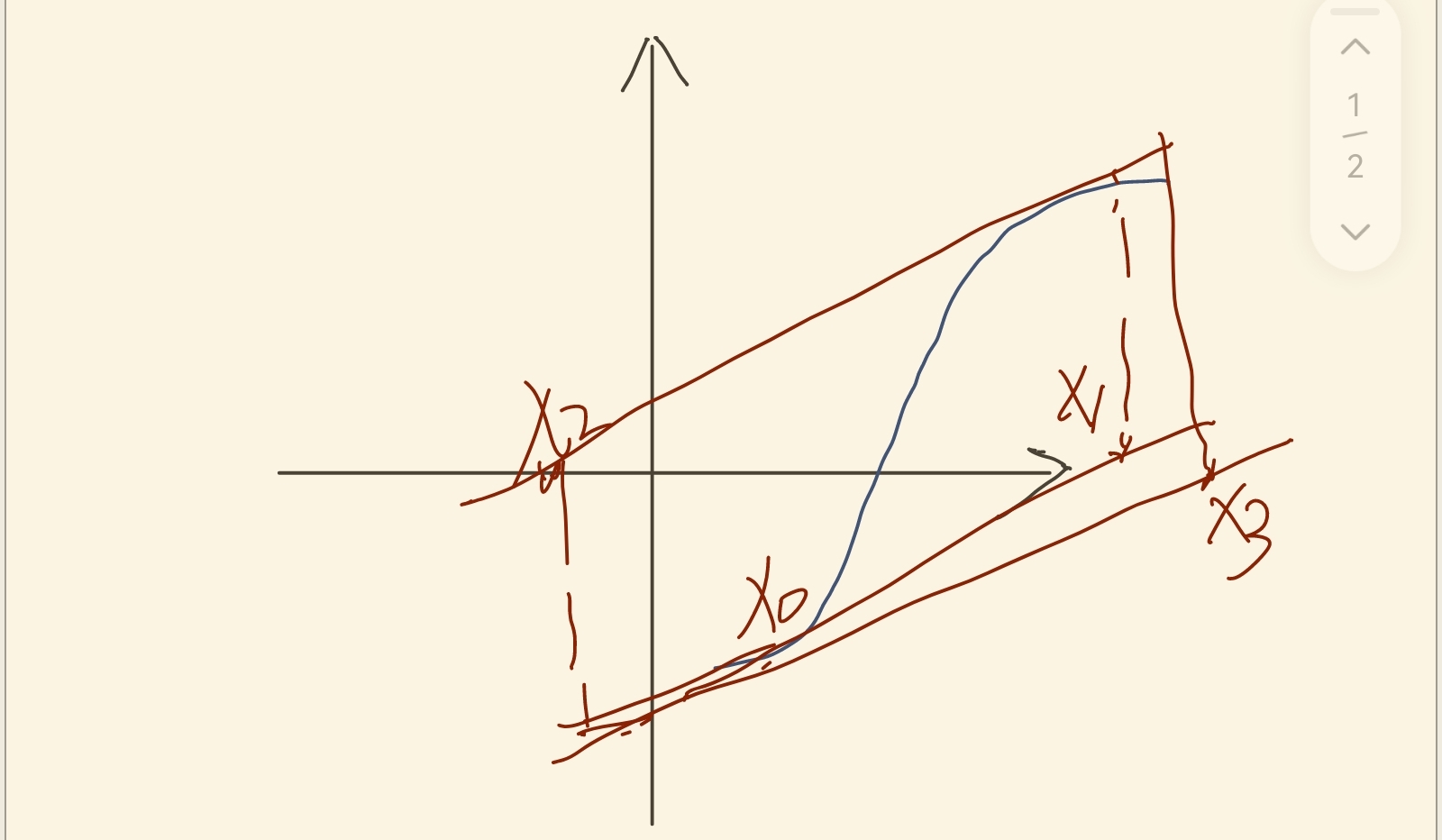
考虑到 $F(t)^{'} 一定有 $ $F(t)^{'} > 0$, 但如果 $F(t)^{''}$ 不能处处大于 0，可能为正也可能为负，此时可能搜索区域会在迭代中越界。(牛顿迭代法在二阶导不处处为正时本身就可能不收敛在鞍点附近震荡)。
文中给出的解决方案是将牛顿迭代和二分混合使用，当超越搜索区域时，就选择区域中点，然后继续迭代计算，因为有二分算法保证，且原范围内一定有 0 解，因此这种迭代方案一定能找到近似解。

优点
曲线动态变化一样求解
不需要像 A Primer on Bézier Curves 存储大量数据
缺点
如果是静态曲线，效率应该是不如 A Primer on Bézier Curves 给出的分割近似方案的

参考

A Primer on Bézier Curves
Moving Along a Curve with Specified Speed - Geometric Tools
【数值计算之二】数值积分之牛顿——科斯特公式：梯形、辛普森、辛普森3/8和布尔 & 高斯积分公式：勒让德、切比雪夫、拉盖尔和埃尔米特
曲线上的匀速运动