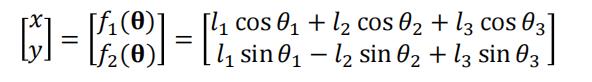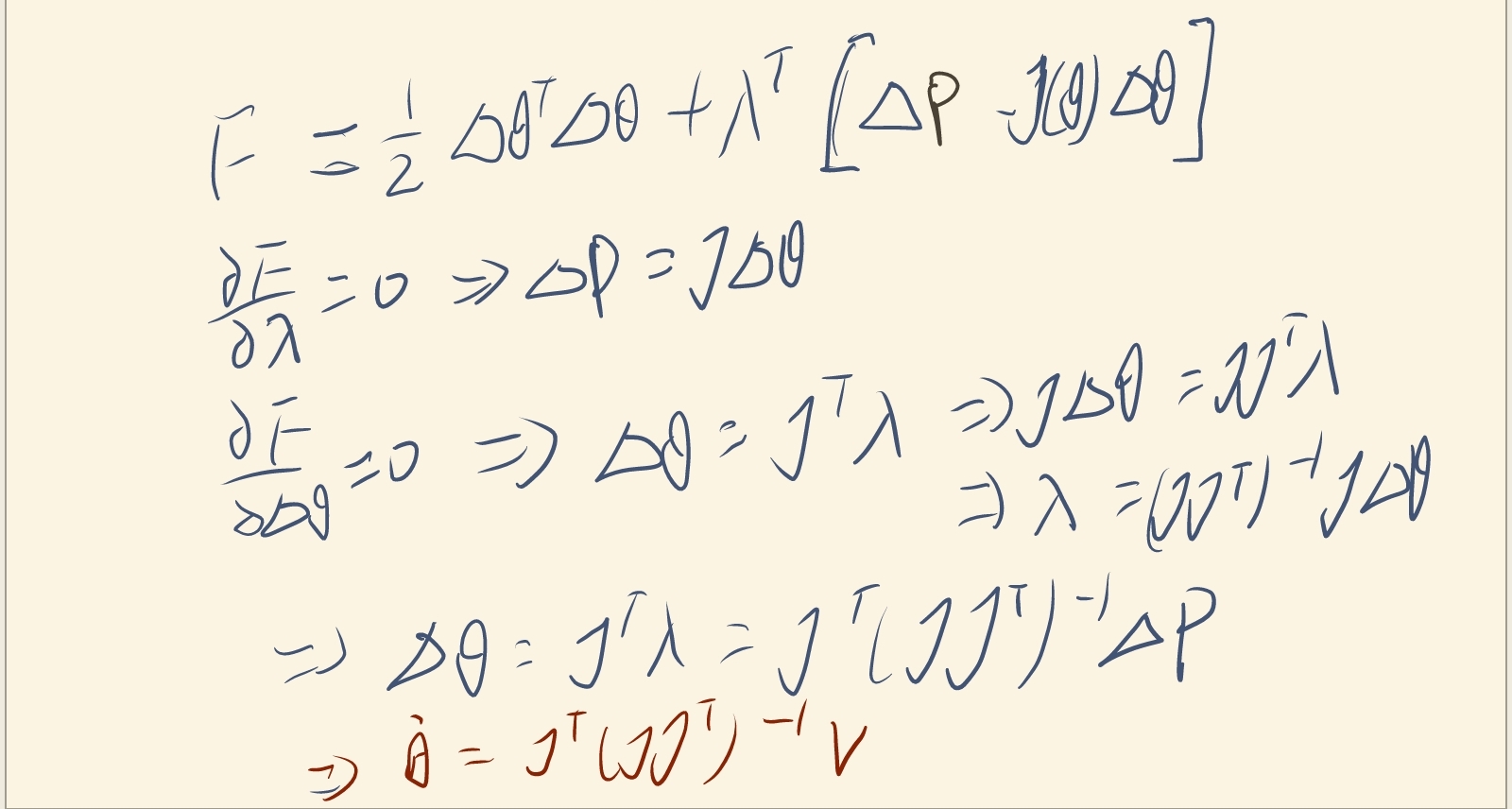IK-JacobianIK

对于多终端 IK 问题，游戏中一般采用 JacobianIK, FABRIK, PBDIK, EXPBDIK，UE 4.26 全身 IK 采用 JacobianIK，UE 5 中采用 PBDIK, 因此有必要了解一下 JacobianIK。为说明 JacobianIK，先从解析法的角度出发计算 IK, 然后再从数值角度求解。

解析法求 IK

给出终端控制器位置，构建终端与关节角度关系，直接求解，这就是解析法，如下图所示

但当关节链比较复杂时，解析解可能不存在，这时就可以采用数值法求解了。

雅克比矩阵数值法求 IK

如果能构建出终端控制器的位置与各个关节旋转角度的关系，即 $f(\theta _{1}, \theta _{2}, \dotsc , \theta _{n}) = E(x,y,z)$, 那么当部分关节发生旋转变化时就能得到终端控制器的变化，这就是雅克比矩阵的作用。
雅克比矩阵：将关节空间的速度(一般是角速度)转换到笛卡尔空间下的速度(一般是线速度)

$\mathbf{E(t)} = f(\mathbf{\theta(t)}) \qquad V = J\dot{\theta}$

逆向雅克比矩阵：笛卡尔空间下的速度转换到关节空间的速度

$\dot{\mathbf{\theta}} = J^{-1}V \qquad \mathrm{d}\mathbf{\theta} = J^{-1} \mathrm{d}\mathbf{E}$

假定现在只有一个末端控制器 E, 那么此时的雅克比矩阵是 $3 \times N$ 矩阵， N 是自由度数目，下面给出一个案列。

雅克比矩阵示例

二维空间下，终端自由度为 2 的关节链，如下图所示

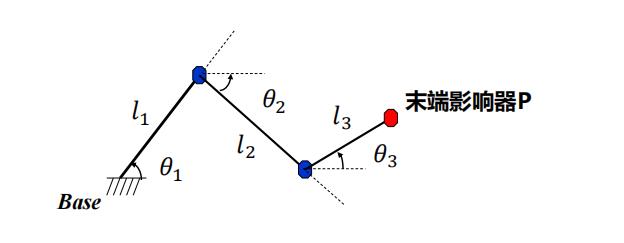
上图有终端坐标 $(x ,y)$ 与各个关节角度的关系

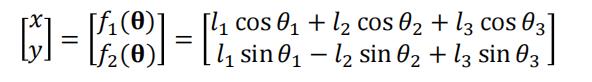
然后求导，得到终端线速度与关节角速度关系式，而它们的映射就是雅克比矩阵，注意
$(x,y) 其实是 (x(t),y(t)), f(\theta) 是 f(\theta(t))$, 然后对 t 求导

修改雅克比矩阵形式

注意到上面雅克比矩阵各个元素使用的是 $\frac{\partial{f(\theta _1 \theta _2 \dotsc \theta _n)} } {\partial{\theta _1}}$ 表示，游戏中不会出现 $\theta$，有必要换个形式表示，游戏里最好的自然是向量了。
考虑刚体上两点，i, j, 它们的角速度分别为 $w_i$, $w_j$, 线速度分别为 $v_i, v_j$, i 到 j 向量为 $p_{ij}$, 有
$v_j = v_i + w_i \times (p_j - p_i)$
现在考虑终端 $E$ 与关节 $i$ , 当关节 $i$ 旋转时它是没有线速度的$v_i = 0$,又因为角速度 $w_i = \dot{\theta}W_i$, $W_i$表示旋转轴, 那么有
$E = v_i + w_i \times (p_E - p_i) = [W_i \times (p_E - p_i)] \dot{\theta}$, 这样也得到了一个将关节角速度转换到终端线速度的表达式，构建出的矩阵就是雅克比矩阵的另一种形式。
但是，这不表明两个矩阵各元素一一对应，现在用另一种方法直接推导原雅克比矩阵元素的另一种形式。

雅克比矩阵元素另一种形式

注意等价无穷小 $\tan \theta = \theta$，$p_4$ 就是终端

雅克比矩阵最后的形式

考虑多终端，多自由度，雅克比矩阵最终形式如下，$w_1,w_2,w_3$ 表示 x,y,z 三个旋转轴$(1,0,0),(0,1,0),(0,0,1)$,如果某个关节 $J_i$ x 轴不能旋转，就让包含 $w1 \times(E - J_i)$ 的元素全部为 0。

使用雅克比矩阵求 IK

上面给出了终端 E 的线速度与关节角速度的关系式 $\mathbf{V} = \mathbf{J}\dot{\pmb{\theta}}$, 如果终端单位时间位移 $\mathbf{V}$，而关节旋转 $\pmb{\dot{\theta}}$ 恰好导致终端单位时间位移 $\mathbf{V}$，这就是为什么求出 $\pmb{\dot{\theta}}$ 再作用到关节上能让终端到达目标位置，现在的问题在于上面的公式不能直接求 $\pmb{\theta}$, 是否要直接用 $\pmb{\dot{\theta}} = \mathbf{J}^{-1} \mathbf{V}$ 求解？

使用雅克比矩阵的转置

上面构建雅克比矩阵采是从物理的角度推导出来的，现在换数学角度推导，为使得终端距离目标位置最近，构建如下误差函数（误差距离的模）
$F=\frac{1}{2} (E_{target} - f(\pmb{\theta}))^T (E_{target} -f(\pmb{\theta})$
为快速到达 $F=0$，那就沿梯度方向，因此对 $F$ 求导有, 注意向量对向量的求导就是雅克比矩阵，得到的形式和上面的相同。

无论从数学的角度看，还是物理的角度看都能得到一个雅克比矩阵，而且上述问题就是最小二乘问题，并且伪逆也和最小二乘有关系。
最终，如果每次迭代让关节旋转 $J^T\mathbf{V}$ 可以让 E 逐步接近目标位置

使用伪逆

当雅克比矩阵 $\mathbf{J}$ 不是方阵时，对 $\mathbf{V} = \mathbf{J}\dot{\pmb{\theta}}$ 两边同左乘 $J^T$ 有
$\mathbf{J}^T\mathbf{V} = \mathbf{J}^T \mathbf{J} \dot{\pmb{\theta}}$
当 J 列满秩时， $\mathbf{J}^T \mathbf{J}$ 可逆
$(\mathbf{J}^T \mathbf{J})^{-1} \mathbf{J}^T \mathbf{V} = (\mathbf{J}^T \mathbf{J})^{-1} \mathbf{J}^T \mathbf{J} \dot{\pmb{\theta}} = \dot{\pmb{\theta}}$
伪逆的物理意义
下面从优化角度说明伪逆的物理意义
现有目标函数 $F(\Delta \pmb{\theta}) = \frac{1}{2} \Delta \pmb{\theta}^T \Delta \pmb\theta$
求在条件 $\Delta \mathbf{p} = \mathbf{J}\Delta \pmb{\theta}$ ($\mathbf{V} = \mathbf{J}\dot{\pmb{\theta}} 换个形式)$ 下什么时候取得最小值
引入拉格朗日常数构建拉格朗日函数
$L(\Delta \pmb{\theta}, \lambda) = \frac{1}{2} \Delta \pmb{\theta}^T \Delta \pmb\theta + \lambda( \Delta \mathbf{p} - \mathbf{J}\Delta \pmb{\theta} )$, 求对 $\Delta \pmb{\theta}$, $\lambda$ 的偏导，并使其为 0，
得到

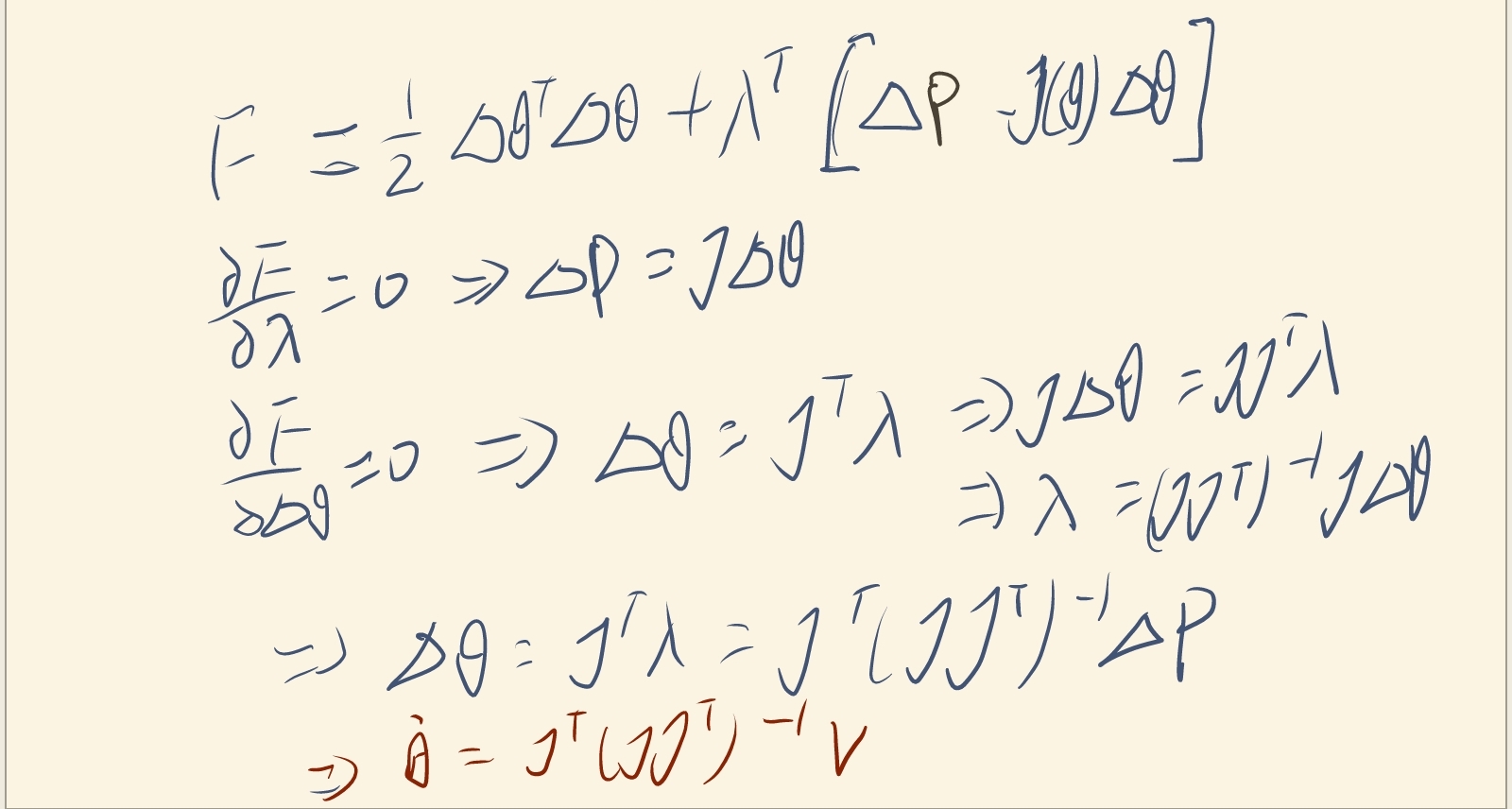
使用雅克比矩阵求解求出的是许多解中的一个，而目标函数 $F(\Delta \pmb{\theta}) = \frac{1}{2} \Delta \pmb{\theta}^T \Delta \pmb\theta$ 保证了当前的解是关节角速度变化最小的解。
最后同样的求出 $\dot{\pmb{\theta}}$ 作用到各个关节上即可完成雅克比 IK，现在的问题在于什么时候，J 会是非列满秩的？注意到雅克比矩阵形式，如果只有两个关节，只考虑旋转轴 x,其形式如下
$\begin{pmatrix} & ((1,0,0) \times (E_1 - J_1)).x & ((1,0,0) \times (E_1 - J_2)).x \\ & ((1,0,0) \times (E_1 - J_1)).y & ((1,0,0) \times (E_1 - J_2)).y \\ & ((1,0,0) \times (E_1 - J_1)).z & ((1,0,0) \times (E_1 - J_2)).z \end{pmatrix}$
显然当 $E_1 - J_1$ 与 $E_1 - J_2$ 同方向时不满足列满秩条件，此时对应的情况是关节连杆平行，或者连杆完全展平如下图所示

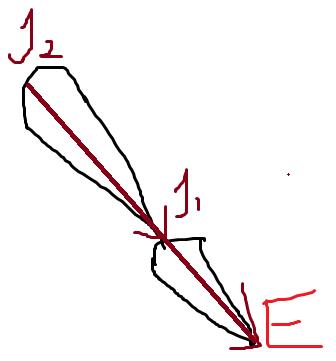
引入阻尼
考虑当 $\mathbf{J}$ 不是列满秩矩阵时，$\dot{\pmb{\theta}} = \mathbf{J}^T (\mathbf{J} \mathbf{J}^T )^{-1} \mathbf{V}$ 无法求解，那么引入一项伪逆敏感程度的附加项 $\lambda I$ 将公式修改为
$\dot{\pmb{\theta}} = \mathbf{J}^T (\mathbf{J} \mathbf{J}^T + \lambda I)^{-1} \mathbf{V}$ ，目的就是尽量要让逆存在。

引入其它控制项
显然还可以引入其它控制项让关节运动看起来更加自然，比如关节 $i$ 朝特定角度偏移
$F(\theta _i) = \alpha _i(\theta _i - \theta _{targeti})$
$\theta _i$: i 关节当前角度
$\alpha_i$: i 关节增益（相当于一个权重，增益越大刚性越强越快逼近目标角度，增益为 0 时控制项失效）
$\theta _{targeti}$: 当前关节目标角度
显然，控制项可以自定义，然后按照上面的条件极值方法求解即可，就看怎么设计让变化更加自然吧。

使用扩展雅克比矩阵

相关论文 Kinematic programming alternatives for redundant manipulator 下载不到，似乎是在原雅克比矩阵基础上扩展行，然后求解，而且雅克比矩阵扩展方案不止这一个，就没看了。

雅克比矩阵方案比较

直接使用转置
优点：简单，数值稳定，不用求逆
缺点：收敛没有那么快，没有控制项
使用伪逆
优点：关节旋转角度最小
缺点：有奇异值问题，要求逆，没有控制项
伪逆并引入阻尼等控制项：
优点：关节旋转角度最小，可以显式的控制关节
缺点：引入了额外的计算
——————————————————————————————————————————

总结

雅克比 IK 做全身 IK 是必然可行的，无论是多骨骼链多终端还是单骨骼链多终端， Jacobian IK 都能求解，而且可以自定义添加控制项让关节运动更加自然。至于求解，通常要么用转置取代逆矩阵，要么求伪逆，一旦要求伪逆就得考虑一下性能开销了，LU, SVD, QR 都有不小的计算开销。另外，雅克比 IK 使用了梯度下降的方法，所以必然存在迭代步长，局部最优等问题。

参考

Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods
Inverse Kinematics Techniques in Computer Graphics_ A Survey
Lecture 16_ Kinematics Transformation_ Part 2
Inverse Kinematics (part 2)