使用雅克比 IK 需要对矩阵求伪逆，性能开销较大，考虑到 PBD 也能完成关节约束，并且不需要求矩阵伪逆，其开销应该会低于 JacobianIK, 因此可以考虑使用 PBD 完成 FullBodyIK。下面先介绍 PBD 算法。

PBD 说明

PBD 算法采用”预测校正“的思路完成模拟，先完成系统在外部作用力，阻尼的计算，得到粒子初步的位置，然后再使用系统内部约束完成位置”校正“。下面直接给出算法步骤
1 初始化粒子数据，质量，速度，起始位置等
2 计算外力对系统的影响
3 计算阻尼对速度的影响
4 依据当前计算出的速度更新粒子预测位置 p
5 生成碰撞约束
6 再考虑系统内部粒子间的约束，求解约束对预测位置 p 校正
7 使用校正位置更新粒子位置以及速度
8 考虑摩擦等因素再次更新粒子速度
从上述步骤来看， PBD 对各个约束分步求解，并且步骤 6 中采用了高斯赛德尔迭代法的思路，对于某一次迭代之前的方程求解会影响到后续方程求解，这样可以加快收敛（对比雅克比迭代）。在这里就是某次迭代中，对某粒子的修正会直接代入下一个粒子的校正求解。

PBD 原理

上面给出了 PBD 算法流程，下面说明算法原理，也就是如何"校正"预测位置。首先说明约束然后说明约束求解。
论文把约束分为等式约束与不等式约束两种
1 等式约束 C(x) = 0 如要求粒子间距离保持不变
2 不等式约束 C(x) >= 0, 如后续的碰撞约束
现在说明如何使让系统稳定下来，也就使用约束校正预测位置以保证约束关系仍然成立

约束求解

当完成外部力，阻尼等计算后，粒子间约束显然很难再满足，如距离约束。但如果强行修改粒子位置，使粒子仍满足约束关系是不够的，最重要的是系统内部约束求解后整个系统应该满足
1 动量守恒
2 角动量守恒
这是因为我们在预测位置时已经计算了外力对系统的影响，因此这里系统不存在外力，并且，当合外外力为 0 时动量守恒，当合外力力矩为 0 时角动量守恒。
那么，现在要做的就是找到校正位移 $\Delta{p}$，有 $C(p +\Delta p) = 0$，且$\Delta p$满足动量与角动量守恒。
对 $C(p)$做一阶泰勒展开将上述方程近似为
$C(p+\Delta p) \approx C(p) + \nabla _p C(p)*\Delta p = 0$

现在，PBD 算法做了一个关键性假设，将 $\Delta p$ 限制在 $\nabla _pC(p)$ 上,以保证动量守恒，这里说下个人的理解。

为什么$\Delta p$ 限制在 $\nabla _pC(p)$ 上可以保证动量角动量守恒

论文中这部分说明如下,主要有两点内容，约束独立于刚体模态，约束梯度与刚体模态垂直。

约束独立于刚体模态
假定所有粒子质量相同，那么对于系统内部约束 C，由于 C 独立于刚体模态（就是刚体运动，即旋转与平移），因此平移旋转这些粒子不改变约束函数的值，也就是 $C(p_1, p_2,\dotsc, p_n)$ 的值。如长度约束 $C(p_1,p_2) = |p_1, p_2| -d$, 对 p_1, p_2 同时做相同的平移旋转变换不改变 $C(p_1,p_2)的值。另外，这里要注意的是举例说明用的是两个粒子的约束，而这里的内部约束 C 针对的是所有粒子 $C(p_1,p_2,\dotsc, p_n)$。
约束梯度与刚体模态垂直
旋转平移不改变约束函数的值，这说明约束梯度 $\nabla {_p}C(p)$ 与刚体运动方向垂直，这点可以从等值线上理解，当粒子沿 C=value 这条等值线运动时，约束函数的值不发生变化，此时，等值线某点切线方向就是运动方向，而梯度与切线垂直，如下图所示。同样的，这里的等值线指的是所有粒子组成的约束函数 $C(p_1,p_2,\dotsc, p_n)$，这点可以参考深入浅出 Nvidia FleX】(1) Position Based Dynamics https://zhuanlan.zhihu.com/p/48737753 的说明。

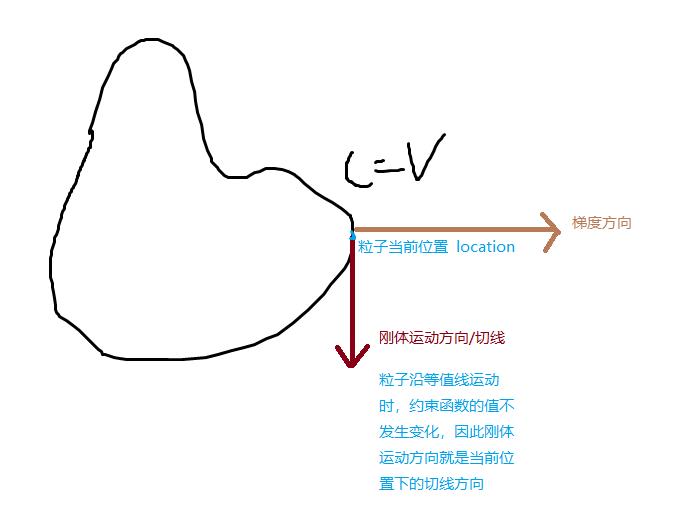
上面得到了重要结论——刚体运动方向与约束梯度方向垂直（刚体运动可以理解成系统运动），因此粒子运动在刚体运动方向上的投影是 0，对刚体运动没有任何影响，自然的，刚体(或者是整个系统)动量与角动量守恒。（系统不会整体发生运动）
这就是个人对论文中校正位移 $\Delta p$ 沿约束梯度方向的理解。另外，动量守恒与角动量守恒还可以从平移不变性和旋转对称性上说明，这点后面再做讨论，现在继续说明约束求解过程。

求解各个粒子校正位移 $\Delta p$

论文给出的多元泰勒展开形式不正确，应该是梯度矩阵的转置
对某一个多元函数泰勒展开形式如下

多个多元函数做泰勒展开
$\begin{pmatrix} C_0(\vec{p}) = C_0(p) + (\nabla _p C_0(p))^T*\Delta p \\ C_1(\vec{p}) = C_1(p) + (\nabla _p C_1(p))^T*\Delta p \\ \cdots \end{pmatrix}$
那么现在有
$C(p+\Delta p) \approx C(p) + (\nabla _p C(p))^T*\Delta p = 0$ （1）
$\Delta p = \lambda \nabla _pC(p)$ （2）
先求出 $\lambda$ 再代入（2）得到

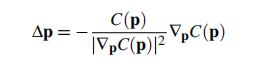
后面推导过程没有什么好说的，直接看论文就好

考虑粒子质量就是用各个粒子质量占总质量百分比进行缩放，现在要说明的是如何求解约束梯度。

约束梯度求解

使用论文中的距离约束 $C(\mathbf{p1}, \mathbf{p2}) = \lvert \mathbf{p1} - \mathbf{p2} \rvert- d$ 距离说明。为了方便说明，首先给出数量函数对向量导数以及矩阵对矩阵的求导定义式。
数量函数对向量的导数
$\mathbf{x} = (x_1,x_2, \dotsc, x_n)^T$, $f(\mathbf{x}) = f(x_1,x_2, \dotsc, x_n)$,有
$\frac{df}{\mathbf{x}} = (\frac{\partial f} {\partial x_1}, \frac{\partial f} {\partial x_2}, \dotsc, \frac{\partial f} {\partial x_n})^T$
矩阵对矩阵的导数

特殊的有

对距离约束求导有

至此，PBD 原理说明结束。
—————————————————————————————————————————————

PBD 额外补充

刚性程度
刚性程度就是粒子跟随刚体运动程度，假设刚体(或者说整个系统)在外力的影响下位移为 S, 那么粒子也发生位移 S, 则表明粒子完全跟随刚体运动，其 stiffness 为 1。
PBD 里最简单的将 stifness 作用到粒子上，就是将校正位移 $\Delta p$ 直接乘以刚性系数 $k$，但考虑第 n 次迭代，某粒子的剩余误差将变为 $\Delta p(1-k)^n$，刚性系数的作用不再是线性的，简单的将刚性系数修改为如下形式即可

$k = 1 - (1-k)^\frac{1}{i} (第 i 次迭代)$

经过 i 次迭代后误差变为 $\Delta p (1-k^{'})^{i} = \Delta {p} (1-k)$
但这样刚性系数 k 直接和迭代次数相关了，也就是迭代次数影响粒子刚性程度，后续 EXPBD 对此做了改进。

碰撞响应

PBD 额外生成 $M_coll$ 个碰撞约束，然后与原本的 $M$ 个粒子间约束一同进行约束求解，如过程 5~6，对应论文中的 8~11。PBD 在每个时间步长迭代中都会生成碰撞约束，并且碰撞约束数量与发生碰撞的粒子数量相关。
5 生成碰撞约束
6 再考虑系统内部粒子间的约束，求解约束对预测位置 p 校正

碰撞检测
如果射线从物体外 p 处发射进入物体内部，找到射线交点 $q_c$ 以及 $q_c$ 处的表面法线 $n_c$, 则有不等式约束 $C(\mathbf{p}) = (\mathbf{p} - \mathbf{q_c})\cdot \mathbf{n_c} \geq 0$
如果射线在物体内，找到 $p_i$ 最近的表面点 $q_s$ 和 $q_s$ 处表面法线 $n_s$, 满足不等式约束
$C(\mathbf{p}) = (\mathbf{p}- \mathbf{q_s})\cdot \mathbf{n_s} \geq 0$
由于上述步骤是在约束求解循环外完成的，所以可能错过一些碰撞（应该是约束校正也可能发生碰撞吧）

碰撞约束案例
假定有三角面 $\mathbf{p_1}, \mathbf {p_2}, \mathbf {p_3}$，现在希望粒子 $\mathbf{q}$ 不会穿过该三角面来到另一侧，则有不等式约束 (前面可带上正负号以确定三角面的哪一面)
$C(\mathbf{q},\mathbf{p_1}, \mathbf{p_2}, \mathbf{p_3}) = (\mathbf{q} - \mathbf{p_1}) \cdot [(\mathbf{p2 - p1}) \times (\mathbf{p_3 - p_1})]$

其他约束

除去上面介绍的距离约束，简单的碰撞约束还存在大量其它的约束，比如弯曲约束，形状匹配约束，这点可以参考
深入浅出 Nvidia FleX】(1) Position Based Dynamics https://zhuanlan.zhihu.com/p/48737753
Games 103 Lecture 02 数学补充（部分） https://zhuanlan.zhihu.com/p/462442629 （给出了一些碰撞检测的方法）

————————————————————————————————————————————

参考

PBD 原论文
啥是PBD (Position Based Dynamics)
猴子都能看懂的position based dynamics笔记
【深入浅出 Nvidia FleX】(1) Position Based Dynamics
Games 103 Lecture 06 Intro to Physics-Based Animation Constraint Approaches